A. 2-3 Moves
문제 설명
0번에서 \(n\)번으로 이동하려고 한다. 현재 위치가 \(x\)일 때, \(x+2\), \(x+3\), \(x-2\), \(x-3\)으로 이동할 수 있다. \(n\)번으로 이동하기 위한 최소 이동 횟수를 출력해야 한다.
알고리즘
일단 \(n\)이 1인 경우는 2칸으로 예외 처리를 하였다. 만약 \(n\)이 3의 배수가 아니라면, \(\frac{n}{3}+1\)번 이동해야 한다. 계속 3칸씩 오른쪽으로 이동하다가, \(n\)을 3으로 나눈 나머지가 1이면 2칸씩 2번, 나머지가 2이면 마지막에 2칸 1번을 뛰어야 하기 때문이다. \(n\)이 3의 배수라면 단순히 3칸씩 계속 뛰면 된다.
따라서 뛰어야 하는 횟수는 \( frac{n+2}{3}\)이 된다. \(n\)이 1인 경우는 예외처리해야 함에 주의하자.
B. Permutation Chain
문제 설명
배열의 고정도를 \(a_i=i\)인 원소의 개수로 정의하자.
처음에 길이가 \(n\)이고, 고정도가 \(n\)인 배열이 주어진다.
이 때, 배열 체인을 만들고자 한다. 체인의 \(i\)번째 배열은 \(i-1\)번째 배열에서 두 원소를 바꾸어 만들 수 있어야 하는 배열이고, 고정도는 \(i-1\)배열보다 작아야 한다.
최대 배열 체인의 길이와 그 때 체인의 각 배열을 출력해야 한다.
알고리즘
먼저 맨 처음에는 무엇을 바꾸더라도 고정도가 2 줄어든다. 따라서 1번과 2번 원소를 바꾼다.
그 이후 \(i\)번째에는 \(i\)번과 \(i+1\)번 원소 원소를 바꾸면 고정도가 1 줄어든다.
따라서 배열 체인의 최대 길이는 \(n\)이고, 단순히 \(i\)와 \(i+1\)번째 원소를 바꿔주면서 출력하면 된다.
C. Robot in a Hallway
문제 설명
\(2 \times m\) 크기의 배열이 주어진다. 배열의 각 값은 0 이상 \(10^9\) 이하인 정수이다. 한 칸을 이동하는 데에는 1초가 걸리며, 각 배열에 적힌 값은 해당 칸이 이동할 수 있게 열리는 시간을 의미한다. 따라서 배열에 적힌 칸이 10이라면, 10초 후 해당 칸이 열려 11초에 해당 칸으로 이동할 수 있게 된다.
\((1,1)\)에서 시작해 모든 칸을 방문하는 데 걸리는 최소 시간을 출력해야 한다.
알고리즘
관찰을 해보면, 모든 칸을 방문하기 위해서는 아래 그림처럼 위 아래를 왔다갔다 하다가 맨 오른쪽 끝으로 간 뒤, 맨 왼쪽 끝으로 돌아오는 방법밖에 없다.
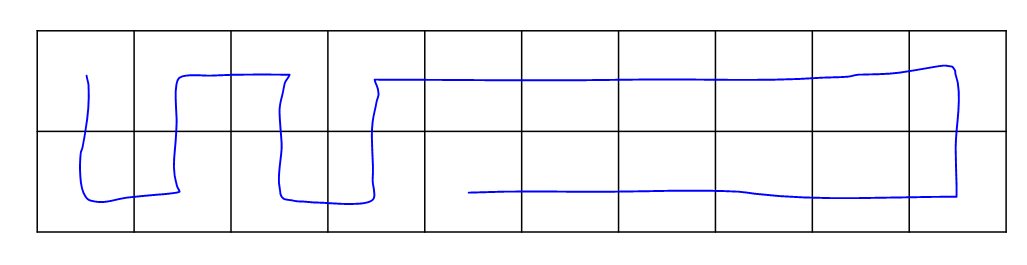
따라서 지그재그로 이동하면서, 맨 오른쪽 끝으로 간 후, 맨 왼쪽으로 돌아오는 데 걸리는 시간을 계산해줘야 한다. 그냥 계산하게 되면 \(O(m^2)\)이 되므로 전처리가 필요하다.
특정 칸에서 맨 오른쪽으로 가는 데 걸리는 시간과 맨 오른쪽에서 특정 칸으로 가는 데 걸리는 시간을 \(O(1)\)에 계산할 수 있다.
먼저 원래 주어진 배열을 \(a_{ij}\)라 하고, 새로운 배열 \(b_{ij} = a_{ij}+j\)로 정의하자.
그렇다면, \((i, j)\)에서 \((i, m)\)으로 가는 데 걸리는 시간은 \(\max_{k\in [j,m]} b_{ik} - j + 1\)이 된다.
따라서 \(b\) 배열의 max값을 전처리하면 이를 \(O(1)\)안에 구할 수 있다. 맨 오른쪽에서 특정 칸으로 가는 데 걸리는 시간도 비슷한 방법으로 구할 수 있다.
따라서 지그재그로 이동하면서 돌아오는 데 걸리는 시간을 \(O(1)\)로 계산하면서 걸리는 시간을 모두 구한 뒤, 그 중 최솟값을 출력하면 된다.
D. Chip Move
문제 설명
0번 칸에서 처음에는 \(k\)의 배수만큼 오른쪽으로, 그 이후에는 \(k+1\)의 배수만큼 오른쪽으로 이런 식으로 이동할 때, \(0\)번칸에서 \(n\) 이하의 모든 자연수 \(i\)에 대해 \(i\)번 칸으로 이동하는 경우의 수를 출력해야 한다. \( n\)은 20만 이하의 자연수이다.
알고리즘
먼저 시간복잡도를 생각하지 않고 점화식을 세워보자.
\(dp[i][j]\)를 \(i\)번 이동해서 \(j\)번 칸으로 이동하는 데 걸리는 시간으로 정의하자.
그렇다면 초기값은 \(dp[0][0] = 0\)이고, 점화식은
\(dp[i][j] = \sum_{a=0}^{\infty} dp[i - 1][j - (k + i - 1) * a]\)가 된다.
이동 횟수는 아무리 커도 700회를 넘지 못한다. \(n=200,000\)이고, \(k=1\)인 경우에도 1칸, 2칸, ... 이런 식으로 최소한으로 점프해도 약 633칸이면 위치가 \(n\)을 넘어가기 때문이다.
하지만 그럼에도 \(dp\)를 위한 공간 복잡도는 \(O(nlogn)\)이고, 시간 복잡도는 이보다 크다. 따라서 시간과 공간 모두를 줄일 방법이 필요하다.
시간의 경우, dp식을 살짝 바꾸어서 처리할 수 있다. 먼저, \(k + i - 1\)의 배수의 칸을 뛰는 것이 아니라, \(k + i - 1\)씩 여러 번 뛰는 것으로 생각하면,
dp식은 \(dp[i][j] = dp[i][j - k] + dp[i - 1][j + k]\)로 바뀌게 된다. 이렇게 계산하면 \(O(nlogn\)으로 시간 복잡도는 만족하게 된다.
공간의 경우도 \(dp[i]\)를 계산하기 위해서는 \(dp[i-1]\)만 필요로 하므로, \(dp[i-1], dp[i]\)만 저장하는 방식으로 공간 복잡도도 \(O(n)\)으로 줄일 수 있다.
E. Swap and Maximum Block
문제 설명
\(2^n\) 길이의 배열이 주어진다. 이 배열에서 총 \(q\)개의 쿼리가 주어진다. 쿼리는 \(k\)라는 0 이상 \(n\) 미만의 정수로 주어진다.
만약 k가 0이라면 1번, 2번 원소 swap, 3번, 4번 원소 swap, ...
k가 1이라면 1번, 3번 swap, 2번, 4번 swap, 5번, 7번 swap, 6번 8번 swap, ....
와 같이 i번째 원소와 \(2^k\)번째 원소를 swap한다.
이렇게 swap한 후 연속 부분합 중 가장 큰 값을 출력해야 한다.
swap으로 변경된 배열은 영구적으로 유지된다.
알고리즘
먼저 배열의 위치를 변경하지 않을 때에는 흔히 금광 세그라고 말하는 기법을 사용하여 부분합의 최댓값을 구할 수 있다.
하지만 이 문제는 배열의 값이 아닌 배열의 위치를 바꾸는 과정이라 어려움이 많다.
일단 주어진 처음 배열로 세그먼트 트리를 구성해둔다. 이제 각 쿼리가 주어질 때마다 세그먼트 트리의 모든 정점을 업데이트 해야 한다. i번 쿼리를 \(q_i\)라고 하고, 세그먼트 트리의 루트의 높이를 0이라 하자. 그렇다면 \(q_i\)를 처리하기 위해서는 높이가 \(n - q_i - 1\)인 정점의 왼쪽 자식와 오른쪽 자식의 위치를 바꾼 뒤, 높이가 \(0\)인 정점까지 차례대로 모두 업데이트 해줘야 한다. 만약 \(q_i\)가 0인 쿼리가 많이 들어오면 시간복잡도는 \(2^nq\)로 시간초과가 발생한다.
하지만 쿼리를 다른 관점으로 바라보면, 시간복잡도를 줄일 수 있다. 먼저 i번째 쿼리를 풀기 위한 세그먼트 트리의 상태를 \(s_i\)라 정의하자. \(s_i\)의 \(j\)번째 bit가 켜져있다면, 높이가 \(j\)인 정점의 자식은 좌우가 바뀌었다는 의미이다.
그렇다면 \(s_i = 2^{n - q_1 - 1} \oplus 2^{n - q_2 - 1} \oplus .... \oplus 2^{n - q_i - 1}\)가 된다. \(\oplus\)는 xor연산을 의미한다.
\(i\)번째 쿼리를 해결하기 위해서는 세그먼트 트리를 \(s_i\) 상태로 만들고 루트의 최대 부분합을 읽어와야 한다.
이 때, 트리의 상태를 \(s\)에서 \(s'\)으로 만들기 위해서 어떤 정점들은 업데이트해야 하는 지 생각해보자.
\(s\)와 \(s'\)에서 다른 bit가 여럿 존재할 것이다. 이 중에서 가장 나중 bit를 k번째 bit라고 하자. 그렇다면 세그먼트 트리에서 높이가 \(k\)보다 큰 정점들은 업데이트할 필요가 없다. 따라서 \(s\)를 \(s'\)으로 바꾸기 위해 필요한 시간 복잡도는 \(O(2^k)\)이 된다.
이제 쿼리의 순서를 적절하게 배열해서 시간복잡도를 줄일 수 있다. 쿼리의 순서를 \(s_i\)가 커지는 순서로 정렬을 해보자.
그렇다면 \(s_i\)에서 \(s_{i+1}\)로 세그먼트 트리의 상태를 바꿀 때 가장 나중으로 다른 bit가 \(n - 1\)번째인 경우는 최대 1번 존재한다. \(n - 2\)번째인 경우는 최대 2번, \(n - 3\)인 경우는 최대 3번 ... \(0\)번째인경우는 최대 \(n\)번 존재한다. 가장 나중으로 다른 bit가 \(k\)인 경우는 최대 \(2^{n - k}\)번 존재하고, 세그먼트 트리의 상태를 바꾸기 위해 필요한 시간 복잡도는 \(O(2^k)\)이므로, 모든 쿼리를 처리하는 데 필요한 시간 복잡도는 \(\sum_{k=1}^{n}2^{n-k} \times O(2^k) \) = \(O(n2^n)\)이다. 따라서 제한시간안에 모든 쿼리의 답을 구할 수 있다.
'Algorithm > Codeforces' 카테고리의 다른 글
| Dytechlab Cup 2022 (Codeforces) (0) | 2022.10.08 |
|---|---|
| Educational Codeforces Round 135 (0) | 2022.09.09 |
| Codeforces Round #806 (Div. 4) (0) | 2022.07.13 |
| Codeforces Round #805 (Div. 3) (0) | 2022.07.11 |
| Codeforces Round #789 (Div. 1) (1) | 2022.05.09 |