A. Six Characters
1) 문제 설명 + 알고리즘
길이가 3이하인 문자열 \( s\)가 들어온다.
문자열 \( s\)를 \( \frac{6}{len(s)} \) 번 출력하면 된다.
B. At Most 3 (Judge ver.)
1) 문제 설명
\(N \leq 300 \)개의 숫자가 주어진다.
이 중 최대 3개의 숫자를 골라서 합이 \( W \)이하로 만들 때, 가능한 합의 경우의 수를 출력하는 문제이다.
2) 알고리즘
\( O(N^3) \) 으로 모든 가능한 합 계산하고, 중복 제외한 뒤 개수를 출력한다.
C. Poem Online Judge
1) 문제 설명 + 알고리즘
N개의 문자열과 정수 쌍 \( (S, T) \)가 주어진다.
set으로 문자열 중복 체크해주고, 처음 나오는 것들 중에서 \( T\)가 최대인 것을 출력하면 된다.
D. At Most 3 (Contestant ver.)
1) 문제 설명
입력으로 \(W \leq 1,000,000\) 가 주어진다. 조건을 만족하도록 \(N \leq 300 \)개의 숫자 \( A \)를 출력하는 문제이다.
\( A \) 중 3개의 원소를 골라 합이 \( n\)이 될 수 있도록 하면 \( n\)을 좋은 자연수라 한다. \( 1\)이상 \( W \)이하의 모든 자연수가 좋은 정수가 되도록 해라.
2) 알고리즘
배열 A를 다음과 같이 출력한다.
1, 2, 3, ... 98, 99, 100, 200, ..., 9800, 9900, 10000, 20000, 30000, ... 98000, 99000, 100000
이렇게 1 이상 99이하인 수 99개, 100 이상 9,900 이하인 수 99개, 10,000 이상 990,000 이하인 수 99개를 배열 \( A \)에 추가해주면, 각 묶음에서 2자리 숫자를 표현할 수 있으므로 1 이상 999,999 이하의 모든 수를 표현할 수 있다. 그리고 1,000,000을 표현하기 위해 배열 \( A \)에 1,000,000를 추가한다.
E. Tahakashi and Animals
1) 문제 설명
총 \(N \leq 3 \times 10^5 \)마리의 동물이 주어진다. 비용 \( A_i\)를 써서 \(i \)번, \(i+1\)번 동물에게 먹이를 줄 수 있다. 이 때, \(A_N\)은 \(1\)번, \(N\)번 동물에게 먹이를 주는 비용이다. 최소한의 비용으로 모든 동물에게 먹이를 주는 문제이다.
2) 알고리즘
일단 비용 \( A_N\)을 고려하지 않고 \(dp\)식을 세워보자.
\(dp[a][0] = a - 1\)번 동물까지 먹이를 주고, \(a\)번 동물에게는 먹이를 주지 않을 때의 비용
\(dp[a][1] = a\)번 동물까지 먹이를 주는 비용
으로 정의한다.
그렇다면 아래의 식이 성립한다.
\( dp[a][0] = dp[a-1][1]\)
\( dp[a][1] = \min(dp[a-1][0], dp[a-1][1]) + A[a-1] \)
이 때, 비용 \(A_N\)을 써서 \(1\)번과 \(N\)번 동물에게 먹이를 주는 경우와 주지 않는 경우를 각각 고려해서 계산하면 된다.
\(1\), \(N\)번 동물에게 먹이를 주지 않는 경우, 초항과 답은 아래와 같고,
\(dp[1][0] =0, dp[1][1] = \infty, ans_1 = dp[N][1]\)
\(1\), \(N\)번 동물에게 먹이를 주는 경우, 초항과 답은 아래와 같다.
\(dp[1][0] =0, dp[1][1] = 0, ans_2 = min(dp[N-1][1], dp[N][1])+A[N]\)
두 정답 중 작은 답을 출력하면 된다.
F. Two Spanning Trees
1) 문제 설명
정점이 \(N \leq 2\times 10^5\)개인 무방향 단순 연결 그래프 \(G\)가 주어진다.
이 때, \(N-1\)개의 간선만 남겨서 아래의 조건을 만족하는 두 그래프를 만들면 된다. 아래 설명은 루트 정점을 \(1\)로 하였을 때 기준이다.
\( T_1: T_1\)에 없고 \(G\)에만 있는 간선 \( (u, v)\)에 대해 \(u\) 또는 \(v\)가 다른 하나의 조상이어야 한다.
\( T_2: T_2\)에 없고 \(G\)에만 있는 간선 \( (u, v)\)에 대해 \(u\) 또는 \(v\)가 다른 하나의 조상이면 안된다.
2) 알고리즘
방향이 없는 그래프에서 DFS를 수행하면 cross edge가 없고, BFS를 수행하면 back edge(또는 front edge)가 존재하지 않는다. 따라서 \(T_1\)은 DFS후 생성되는 트리이고, \(T_2\)는 BFS후 생성되는 트리이다. 즉, DFS, BFS를 진행하고 결과를 출력하면 된다.
G. Intersection of Polygons
1) 문제 설명
먼저 점의 수가 \(N \leq 50\)인 볼록 다각형이 주어진다. 이 때, 이 볼록 다각형의 복제본을 총 \( M \leq 2\times 10^5 \)개 만든다. \(i\)번째 복제본 \(P_i\)는 주어진 볼록 다각형을 \( (u_i, v_i)\)만큼 이동시킨 것이다.
이제 총 \(Q \leq 2 \times 10^5 \)개의 쿼리가 주어진다. \(i \)번째 쿼리는 \((x_i, y_i)\)가 모든 \(M\)개의 복제본 다각형 안에 있는 지를 묻는 문제이다.
2) 알고리즘
일단 복제본이 하나인 경우에는 간단하게 풀 수 있다. 볼록 다각형의 모든 \( N\)개의 선분에 대해 선분과 \(x_i, y_i\)가 반시계 방향에 있다면 점 \(x_i, y_i\)는 볼록 다각형 안에 있다.
복제본이 \(M\)개인 경우에는 문제를 푸는 것이 어려워진다. 원본의 특정 선분에 대해 \(M\)개의 복제본에 대해서 모두 반시계 방향에 있는 지를 검사해야 한다.
관찰을 해보면 모든 \(M\)개의 복제본에 대해 모두 반시계 방향에 있는 지 검사할 필요가 없다.
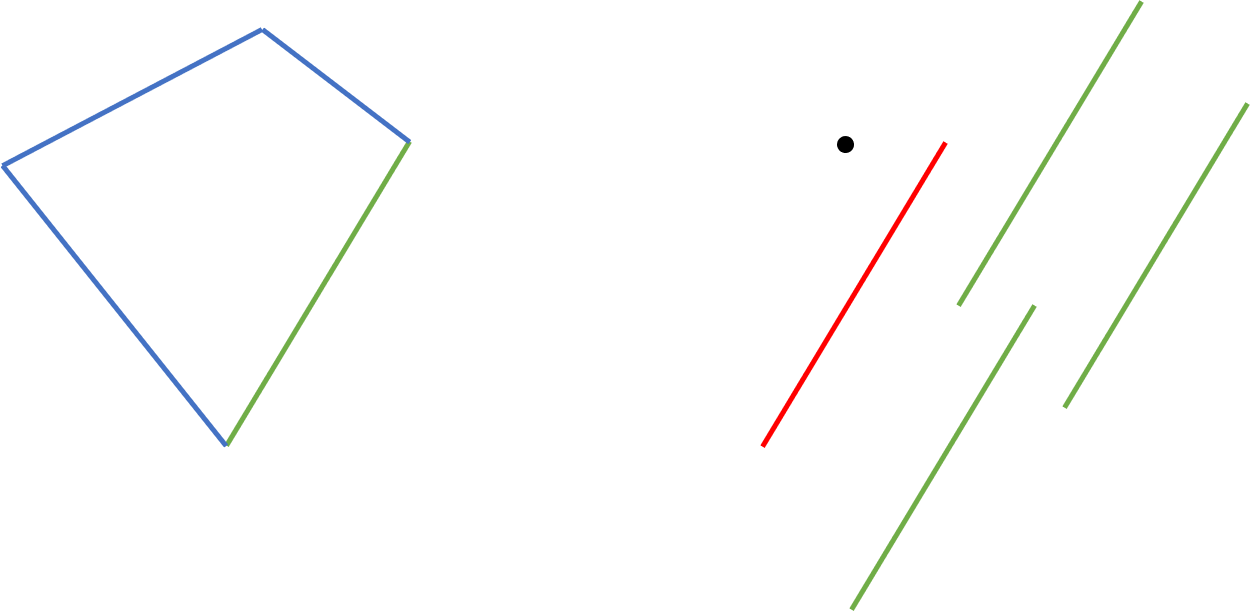
위와 같이 다각형에서 초록색 선분의 복제본 \(M\)개에 대해 모두 반시계 방향을 검사할 필요 없이 빨간색 선분에 대해서만 반시계 방향 검사를 해주어도 충분하다.
따라서 각 선분에 대해 \( M\)개의 복제본을 만들고 어떤 복제본만 검사해주면 되는 지 찾아주면 된다. 이는 반시계 검사를 이용해서 \( O(M) \)안에 찾을 수 있다.
따라서 총 \( O(NM) \)의 전처리로 우리가 검사해야 할 \(N\)개의 선분을 찾을 수 있고, 각 쿼리는 이 선분들에 대해서만 검사해주면 되므로, 모든 쿼리를 \(O(QN) \)의 시간복잡도로 처리할 수 있다.
'Algorithm > Atcoder' 카테고리의 다른 글
| AtCoder Beginner Contest 277 (0) | 2022.11.13 |
|---|---|
| AtCoder Beginner Contest 265 (0) | 2022.08.23 |
| AtCoder Beginner Contest 264 (0) | 2022.08.14 |
| AtCoder Beginner Contest 258 (1) | 2022.07.02 |
| AtCoder Beginner Contest 257 (0) | 2022.06.29 |